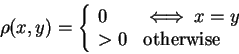There are three properties
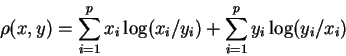
a distance measure? Constraints:
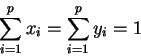
and xi, yi > 0.
-
Rewriting
 as
as
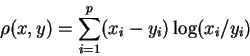
it's pretty obvious that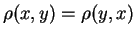 and that
and that
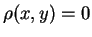 iff x=y. But is it non negative? There's
LOTS of ways to do this. There's a sleight-of-hand way using
a useful factoid that
iff x=y. But is it non negative? There's
LOTS of ways to do this. There's a sleight-of-hand way using
a useful factoid that
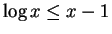 .
But that's another story.
Here's the easy way - notice that
.
But that's another story.
Here's the easy way - notice that
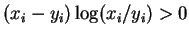 is always greater than zero for
is always greater than zero for
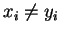 and identically zero
if
xi = yi. SO the beast is non-negative.
and identically zero
if
xi = yi. SO the beast is non-negative.
-
Now the fun begins - is the ``triangle inequality'' satisfied?
We need to compare
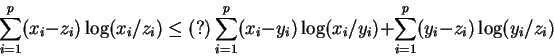
Splitting things up and dragging to one side we obtain
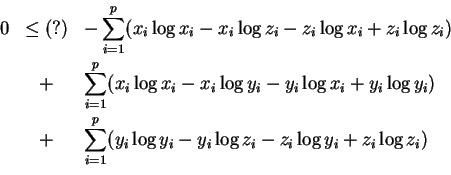
Simplifying
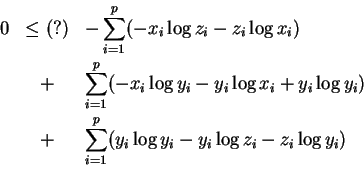
Grouping terms
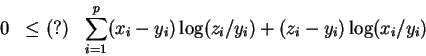
As you can see, this is tricky for general p, at least on short notice. So we now invoke p=2 along with the contraints to obtain,
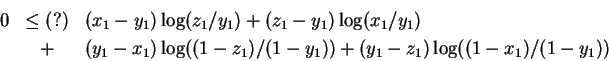
Regrouping
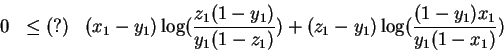
Let's make x1 > y1 and z1 < y1. The first term is negative because the term inside the log is smaller than 1. The second term is negative because the leading factor is negative while the term inside the log is greater than 1. So the RHS can be made negative.Thus, when all is said and done, this is not a distance measure for p=2. I also suspect that one can find similar examples for larger pbut I did not dig into it.
(The above was done quickly so please check the algebra for this part).
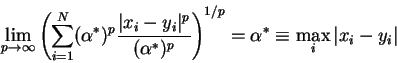
Well
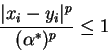
owing to the definition of
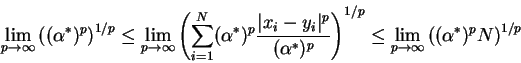
or
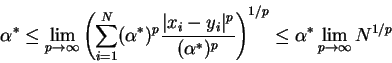
The result follows since